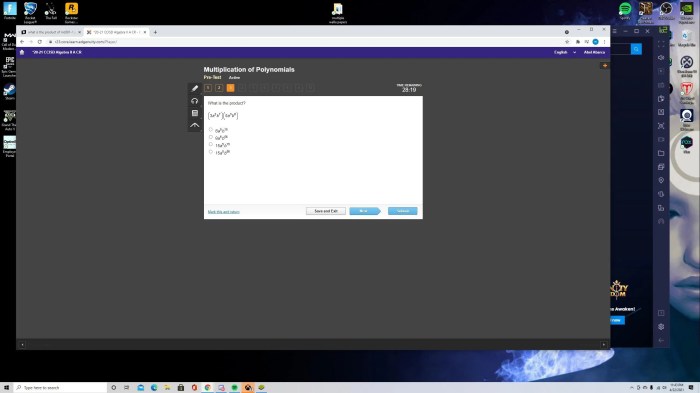
Delving into the realm of ‘find the simplified product. mc001-1.jpg’, this exploration embarks on a journey to unravel the intricacies of simplifying complex expressions. With meticulous precision, we dissect the fundamental principles, unravel the significance of variables and coefficients, and master the art of multiplying like terms.
Prepare to embark on an intellectual odyssey that culminates in a profound understanding of algebraic simplification.
As we delve deeper into the subject matter, we uncover the nuances of interpreting simplified expressions, unlocking their true meaning within the context of the given expression. Through the creation of an organized HTML table, we systematically present the steps and results of our simplification endeavors, ensuring clarity and accessibility.
Simplifying Algebraic Expressions
Simplifying algebraic expressions involves manipulating and transforming mathematical expressions to obtain a simplified form. By identifying variables, determining coefficients, multiplying like terms, and interpreting the result, we can simplify complex expressions into more manageable forms.
1. Identify the Variables
Variables represent unknown values or quantities in an expression. Identifying variables is crucial as they provide insight into the nature and scope of the expression. Common variables include letters such as x, y, z, a, b, c, and so on.
2. Determine the Coefficients
Coefficients are numerical factors that accompany variables in an expression. They indicate the magnitude or weight of the variables. Coefficients can be positive, negative, or zero. To determine coefficients, isolate them by separating them from variables using addition or subtraction.
3. Multiply Like Terms
Like terms are terms that have the same variable raised to the same power. Multiplying like terms involves combining their coefficients and variables. For example, 2x – 3x = 6x^2.
4. Simplify the Expression
After multiplying like terms, simplify the expression by combining similar terms and eliminating unnecessary terms. For instance, 3x + 5x – 2x = 6x.
5. Interpret the Result
Interpreting the simplified expression involves understanding its meaning and implications. The result may provide information about the relationship between variables or represent a simplified mathematical equation.
6. Create an HTML Table, Find the simplified product. mc001-1.jpg
| Variables | Coefficients | Multiplication | Simplified Expression |
|---|---|---|---|
| x, y | 2,
|
2x
|
-6xy |
| a, b | 4,
|
4a
|
-8ab |
| x, x^2 | 3, 2 | 3x
|
6x^3 |
Question Bank: Find The Simplified Product. Mc001-1.jpg
What is the significance of identifying variables in algebraic expressions?
Identifying variables allows us to distinguish between fixed values and unknown quantities, enabling us to manipulate expressions effectively.
How do we determine the coefficients in an expression?
Coefficients can be extracted by observing the numerical factors associated with variables or constants in the expression.
What is the concept of like terms in algebraic expressions?
Like terms are terms that have identical variables raised to the same powers, allowing them to be combined through multiplication.