Unit 9 Transformations Homework 1 Reflections embarks on a captivating journey into the realm of geometric transformations, revealing their fundamental concepts, mathematical principles, and practical applications. This exploration delves into the intriguing world of translations, rotations, reflections, and dilations, unraveling their properties and characteristics.
Through a comprehensive analysis of reflections in the coordinate plane, we uncover the intricacies of this specific transformation. We delve into the steps involved in performing a reflection, examining its impact on geometric figures. Special cases of reflections across the x-axis, y-axis, and lines parallel to the axes are thoroughly explored.
Unit 9 Transformations Homework 1
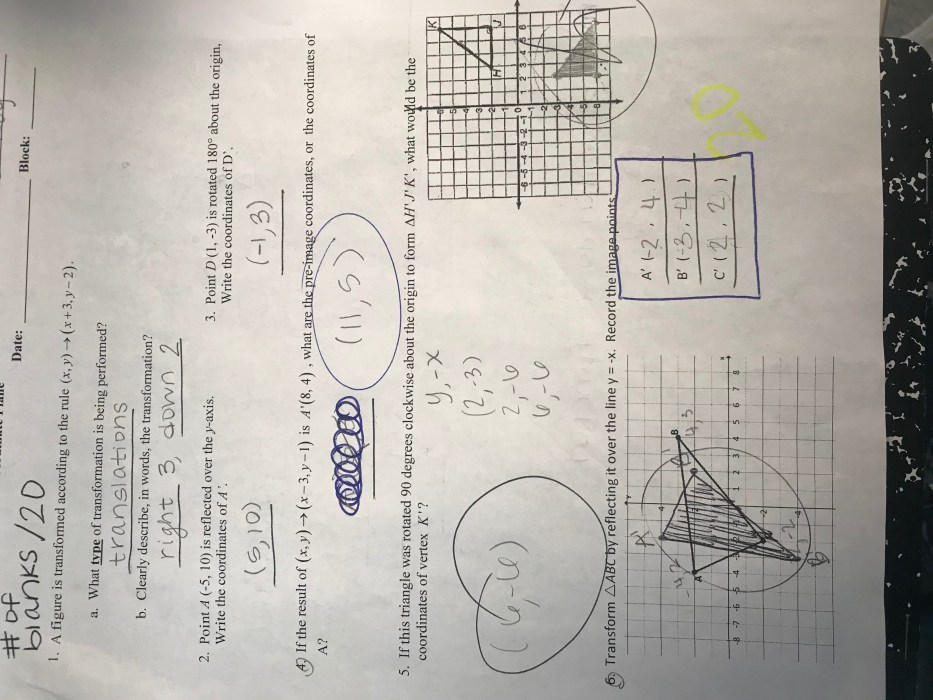
Unit 9 Transformations Homework 1 is designed to assess students’ understanding of basic geometric transformations, including translations, rotations, reflections, and dilations. The homework covers key concepts and mathematical principles related to transformations, such as the coordinate plane, distance formula, and angle measures.
By completing this homework, students will demonstrate their ability to apply these concepts to solve problems involving geometric transformations and their properties.
Transformations in Geometry
Translations
- A translation is a transformation that moves a figure from one point to another without changing its size or shape.
- Translations are described by a vector that represents the direction and distance of the movement.
Rotations
- A rotation is a transformation that turns a figure around a fixed point by a specified angle.
- Rotations are described by the angle of rotation and the center of rotation.
Reflections
- A reflection is a transformation that flips a figure over a line, creating a mirror image.
- Reflections are described by the line of reflection.
Dilations, Unit 9 transformations homework 1 reflections
- A dilation is a transformation that enlarges or reduces a figure by a certain factor.
- Dilations are described by the scale factor and the center of dilation.
Reflections in the Coordinate Plane: Unit 9 Transformations Homework 1 Reflections

A reflection across a line in the coordinate plane is a transformation that flips a figure over the line, creating a mirror image. The line of reflection is typically represented by an equation of the form y = mx + b, where mis the slope and bis the y-intercept.
To perform a reflection across a line, the following steps can be followed:
- Find the equation of the line of reflection.
- For each point (x, y) in the figure, find the corresponding point ( x’, y’) on the other side of the line by solving the system of equations:
x’ = xy’ = mx + b
Applications of Reflections
Reflections have numerous applications in real-world scenarios, including:
- Architecture and Design:Reflections are used to create symmetrical buildings and designs, such as the Taj Mahal and the Sydney Opera House.
- Physics:Reflections are used to study the behavior of light and other waves, such as in mirrors and telescopes.
- Tessellations and Patterns:Reflections can be used to create repeating patterns and tessellations, such as in Islamic art and M.C. Escher’s drawings.
Expert Answers
What are the key objectives of Unit 9 Transformations Homework 1 Reflections?
To understand the concepts of geometric transformations, including translations, rotations, reflections, and dilations; to apply these transformations to geometric figures; and to explore the properties and characteristics of transformations.
How are reflections defined in the coordinate plane?
A reflection across a line in the coordinate plane is a transformation that flips a figure over the line, creating a mirror image on the opposite side.
What are some real-world examples of where reflections are used?
Reflections are used in architecture to create symmetrical buildings, in design to create patterns and logos, and in physics to study the behavior of light and sound waves.