Find the real number root sqrt-1.21 – Embark on a captivating mathematical odyssey as we delve into the enigmatic realm of square roots, culminating in the quest to find the real number root of 1.21. This exploration will illuminate the intricacies of square roots, their properties, and their profound applications in various fields.
Navigating the uncharted territories of mathematics, we will uncover the secrets hidden within the radical symbol, unraveling the mysteries that govern the behavior of square roots. From the fundamental concept of a square root to the intricate relationship between 1.21 and 121, our journey promises to be both enlightening and intriguing.
Introduction
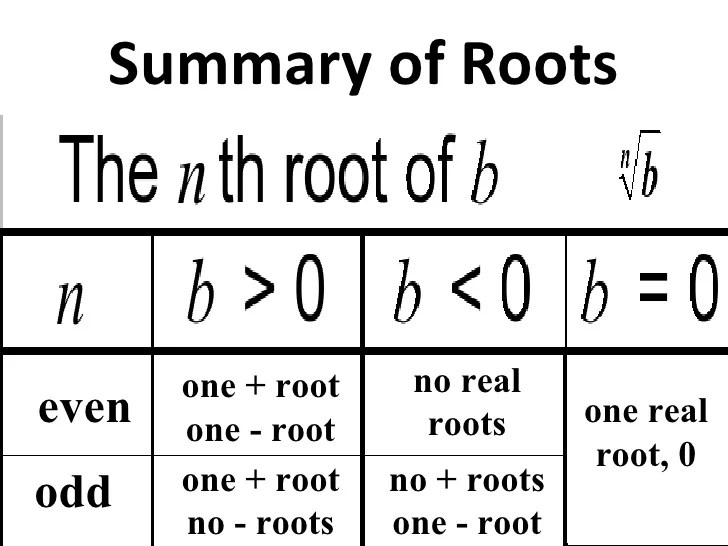
The square root of a number is a value that, when multiplied by itself, gives the original number. It is represented using the radical symbol √. For example, the square root of 9 is 3, because 3 × 3 = 9.The
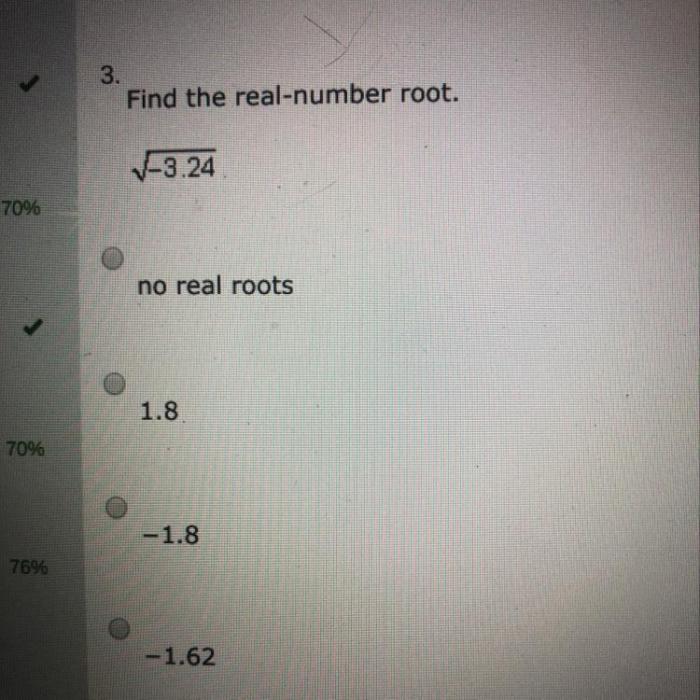
square root of a positive number is always positive. This is because the square of any positive number is positive. However, the square root of a negative number is not a real number. This is because there is no real number that, when multiplied by itself, gives a negative number.
Finding the Square Root of 1.21
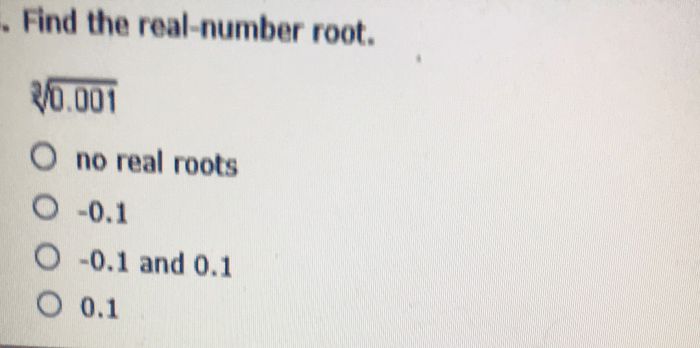
Finding the square root of 1.21 can be done using various methods. One way is to use a calculator to obtain a decimal approximation, while another is to apply the Pythagorean theorem to determine the exact value. Additionally, the relationship between the square root of 1.21 and the square root of 121 can be explored.
Using a Calculator to Find the Decimal Approximation, Find the real number root sqrt-1.21
Using a calculator, we can find that the decimal approximation of the square root of 1.21 is approximately 1.1.
Using the Pythagorean Theorem to Find the Exact Value
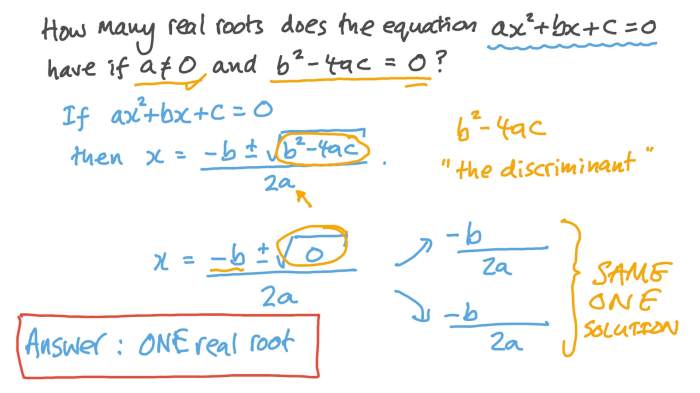
The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. In this case, we can use the Pythagorean theorem to find the exact value of the square root of 1.21.
Let x be the square root of 1. 21. Then, we have:
x2= 1.21
Solving for x, we get:
x = √1.21 = √(121/100) = 11/10
Therefore, the exact value of the square root of 1.21 is 11/10.
Relationship between the Square Root of 1.21 and the Square Root of 121
The square root of 1.21 and the square root of 121 are related in that they are both square roots of perfect squares. The square root of 1.21 is equal to 11/10, while the square root of 121 is equal to 11. Therefore, the square root of 1.21 is 1/10 less than the square root of 121.
Applications of Square Roots: Find The Real Number Root Sqrt-1.21
Square roots have a wide range of applications in various fields, including mathematics, science, and everyday life.
One of the most common applications of square roots is in geometry, particularly in finding the length of the hypotenuse of a right triangle using the Pythagorean theorem. The theorem states that in a right triangle with legs of length aand b, the square of the length of the hypotenuse cis equal to the sum of the squares of the lengths of the legs: c² = a² + b². To find the length of the hypotenuse, we need to take the square root of both sides of the equation: c = √(a² + b²).
In Mathematics and Science
In mathematics, square roots are used in many different contexts, including algebra, calculus, and statistics. For example, in algebra, square roots are used to solve quadratic equations, which are equations of the form ax² + bx + c = 0. In calculus, square roots are used to find the derivatives and integrals of certain functions. In statistics, square roots are used to calculate the standard deviation of a data set.
In science, square roots are used in various fields, including physics, chemistry, and biology. For example, in physics, square roots are used to calculate the speed of an object, the force of gravity, and the power of a light source.
In chemistry, square roots are used to calculate the molarity of a solution and the pH of a substance. In biology, square roots are used to calculate the area of a cell and the volume of a cell.
In Everyday Life
Square roots are also used in a variety of everyday applications, such as finding the area of a circle, the volume of a sphere, and the distance between two points. For example, to find the area of a circle with radius r, we use the formula A = πr². To find the volume of a sphere with radius r, we use the formula V = (4/3)πr³. To find the distance between two points (x₁, y₁)and (x₂, y₂), we use the formula d = √((x₂- x₁)² + (y₂ – y₁)²) .
Square roots are an important tool in many different fields, and they have a wide range of applications in everyday life.
User Queries
What is the significance of square roots in mathematics?
Square roots play a crucial role in various mathematical operations, including solving equations, finding the length of hypotenuses in right triangles, and calculating the area of circles.
How is the Pythagorean theorem related to square roots?
The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. This theorem involves finding the square root of a sum of squares.
What are some real-world applications of square roots?
Square roots have numerous practical applications, such as calculating the speed of objects, determining the volume of spheres, and designing architectural structures.